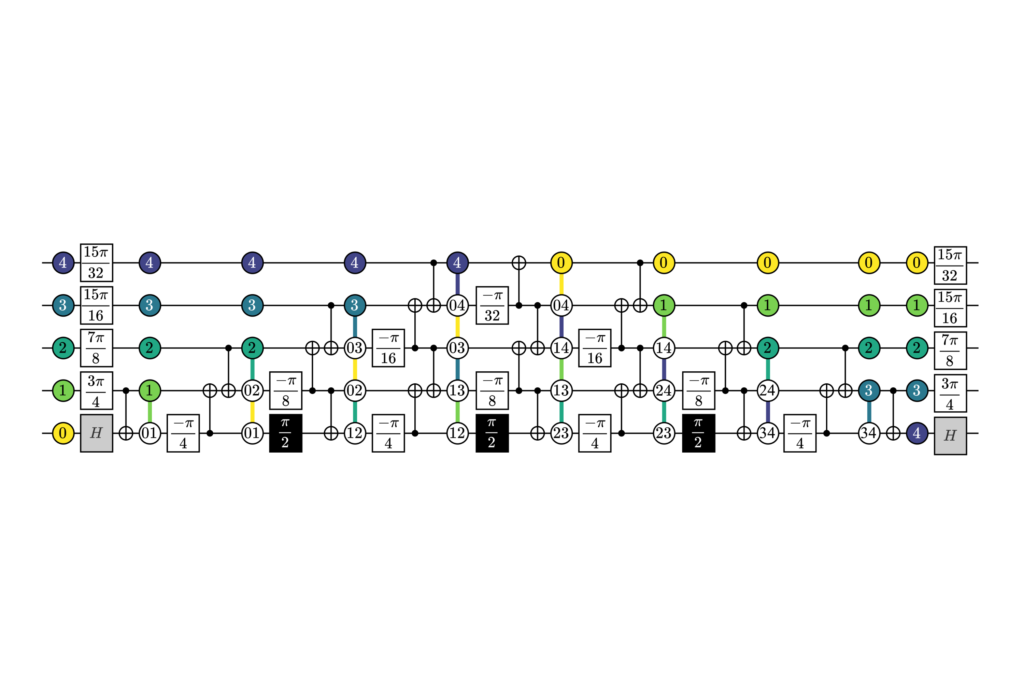
Innsbruck, 16.10.2024. The teams at ParityQC and the University of Innsbruck discovered the most efficient implementation of the Quantum Fourier Transform – one of the most fundamental algorithms in quantum computing – on a linear chain. In the paper “SWAP-less implementation of Quantum Algorithms” they present the novel implementation, which eliminates the need for SWAP or Shuttling operations.
The Quantum Fourier Transform, or abbreviated QFT, is a cornerstone algorithm in quantum computing. It is the basis of several seminal algorithms ranging from Shor’s algorithm, which is one of the grand goals of error-corrected quantum computing, to quantum optimization.
Over the past century, various improvements to the QFT implementation have been suggested, in order to reduce the number of required gates and optimize runtime. This is particularly relevant for quantum systems with limited connectivity, such as a linear chain of qubits. A significant challenge arises from the fact that QFT requires gates to operate between every pair of qubits. On a linear chain, this is not feasible directly, requiring either the movement of quantum information (SWAP operations) or the physical movement of qubits (Shuttling operations).
The ParityQC Architecture eliminates the need for SWAP or Shuttling operations. The teams at ParityQC and the University of Innsbruck have now demonstrated that with the elimination of this overhead it is possible to achieve the most efficient implementation of QFT. In the paper “SWAP-less Implementation of Quantum Algorithms”, the authors (Berend Klaver, Stefan Rombouts, Michael Fellner, Anette Messinger, Kilian Ender, Katharina Ludwig, Wolfgang Lechner) present a new formalism based on tracking the flow of parity quantum information, which is the basis of the implementation. Instead of using SWAP or Shuttling, the method leverages the fact that entangling gates not only manipulate quantum states but can also be exploited to transport quantum information.
This method improves upon all current state-of-the-art implementations of the Quantum Fourier Transform (QFT) on a linear nearest-neighbor architecture, achieving a total circuit depth of 5n−3 and requiring n^2−1 CNOT gates. These two metrics—circuit depth and gate count—are critical for practical implementation. Circuit depth directly impacts the algorithm’s runtime, while minimizing the number of gates is essential since each gate introduces potential errors into the quantum system.
Publication:
Berend Klaver, Stefan Rombouts, Michael Fellner, Anette Messinger, Kilian Ender, Katharina Ludwig, Wolfgang Lechner. SWAP-less Implementation of Quantum Algorithms. arXiv:2408.10907v1 (2024)